음악, 삶, 개발
21. Algorithms and Maps 본문
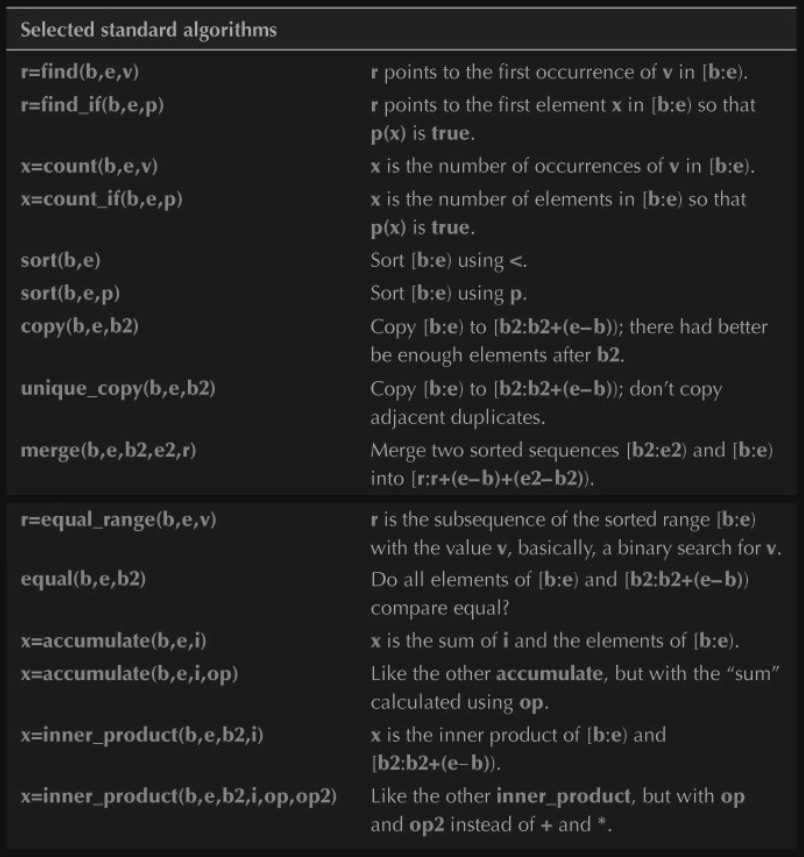
21.1 Standard library algorithms
standard library 는 80가지의 algorithm 을 제공한다.
이중 가장 많이 쓰이는 일부를 소개한다.
standard library 인 algorithm 을 사용할려면 아래와 같이 추가하도록 한다.
#include <algorithm>이 algorithm 들은 1개 혹은 1개 이상의 sequence 를 받는다.
input sequence 는 2개의 iterator 로 정의되며, output sequence 는 첫번째 element 를 나타내는 iterator 에 의해 정의된다.
algorithm 은 일반적으로 함수로 표현된다.
algorithm 은 보통 intput sequence 에서 실패한 것 (failure) 을 input sequence 의 end 를 return 함으로써 report 한다.
예를 들어, find(b,e,v) 함수에서, v 를 찾지못하면 e 를 return 한다.
21.2 The simplest algorithm : find()
틀림없이, 가장 단순하고 유용한 알고리즘은 find() 이다.
find() 는 value 를 받으면 sequence 안에서 이 value 를 가진 element 를 찾아준다.
find() 은 내부는 대략 아래와 같이 구현되었다.
template<typename In, typename T>
In find(In first, In last, const T& val) {
while(first! = last && *first != vale) {
++first;
}
return first;
}우리가 이렇게 find() 의 내부를 굳이 알필요는 없지만,
find() 의 definition 은 많은 유용한 디자인 idea 를 가지고있어서, 내부를 살펴보는것은 많은 도움이 될것이다.
우선, find() 는 2개의 iterator 로 정의된 sequence 를 연산한다.
우리는 half-open sequence [first:last) 에서 val 이라는 값을 찾고있다.
find() 가 결과값으로 return 하는것은 iterator 이다.
결과값은 sequence 에서 val 이라는 값을 가진 가장 첫번째 element (여러개가 발견될수도있기에) 를
가리키거나, last 를 가리킨다.
앞서 말했듯이, last 는 last element 가 아니라 last element 를 넘어선 그 다음 자리다.
find() 가 val 을 발견하지못하였을때 return 하는 것또한 one-beyond-te-last element 를 가리키는 iterator 이다.
이 방식이 STL 에서 가장 많이 쓰이는 "not found" (발견못함) 을 report 하는 방법이다.
find() 는 아래와 같이 사용할수있다.
void f(vector<int>& v, int x) {
auto p = find(v.begin(), v.end(), x);
if (p != v.end()) {
// we found x in v.
}
else {
// no x in v.
}
}위의 코드처럼 generic code 를 작성하고자할때 auto 는 매우 유용하다.
21.2.1 Some generic uses
find() 는 매우 generic 하다.
generic 이 의미하는것은 매우 다른 data types 들을 사용할수있다는것이다.
어떠한 element type 혹은 STL-stlye sequence 든 사용할수있다는것이다.
void f1(vector<int>& v, int x) {
vector<int>::iterator p = find(v.begin(), v.end(), x);
if (p != v.end()) {
// we found x.
}
}
void f2(list<string>& v, string x) {
list<string>::iterator p = find(v.begin(), v.end(), x);
if (p != v.end()) {
// we found x.
}
}이런 식의 flexibility 가 STL 알고리즘이 가지고있는 가장 큰 장점이다.
21.3 The general search : find_if()
우리는 보통 특정 값을 찾지않고, 어떠한 조건에 부합하는 값을 찾는데에 관심이 있다.
예를 들어,
우리는 42 보다 큰 값을 찾기를 원할것이다.
우리는 두개의 문자를 비교하기를 원할것이다.
우리는 홀수(odd)의 첫번째 값을 찾기를 원할것이다.
우리는 주소값으로 "17 Cherry Tree Lane" 이라고 적힌 기록을 찾기를 원할것이다.
find_if() 는 사용자가 정한 기준에 맞는 값을 찾도록해준다.
template<typename In, typename Pred>
In find_if(In first, In last, Pred pred) {
while(first! = last && !pred(*first)) {
return first;
}
}우리는 find _int() 를 통해 아래와 같은 조건들을 포함시킬수있다.
"문자 x 를 포함하는 string"
"42 보다 큰 값"
"홀수인 숫자"
예를 들어, vector 내에서 홀수인 int 를 찾는 code 를 find_if() 를 사용하여 작성해보자.
bool odd(int x) { return x % 2; }
void f(vector<int>& v) {
auto p = find_if(v.begin(), v.end(), odd);
if (p! = v.end()) {
/* we found odd number! */
}
}
다음으로 list 에서 특정값보다 큰 element 를 찾는 코드를 작성해보자.
double v_val;
bool larger_than_v(double x) { return x > v_val; }
void f(list<double>& v, int x) {
v_val = 31;
auto p = find_if(v.begin(), v.end(), larger_than_v);
if (p != v.end()) {
/* we found a value > 31 */
}
v_val = x;
auto q = find_if(v.begin(), v.end(), larger_than_v);
if (q! = v.end()) {
/* we found a value > x */
}
}21.4 Function objects
function object 라는 말 그대로 함수처럼 행동할수있는 객체이다.
우리는 data 를 저장하기위해서는 객체가 필요하다.
예제를 보자.
class Larger_than {
public:
Larger_than(int vv) : v(vv) {} // store the argument
bool operator() (int x) const { return x > v; } // compare
private :
int v;
}
void f(list<double>& v, int x) {
auto p = find_if(v.begin(), v.end(), Larger_than(31));
if (p! = v.end()) {
/* we found a value > 31 */
}
auto q = find_if(v.begin(), v.end(), Larger_than(x));
if (q! = v.end()) {
/* we found a value > x */
}
}위의 코드에서 operator() 를 볼수있는데,
() 를 function call operator 라고 한다.
21.4.1 An abstract view of function objects
function 란 data 를 주위로 운반하기위한 (carry around) 메카니즘이다.
function object 는, 매우 genaral 하고 강력하고 편리한 메카니즘을 제공한다.
function object 의 일반적인 개념을 코드로 살펴보자.
// abstract example of a function obeject
class F {
public :
F(const S& ss) : s(ss) { /* establish initial state */ }
T operator() (const S& ss) const {
// do something with ss to s
// return a value of type T (T is often void, bool, or S)
}
const S&s state() const { return s; } // reveal state
void reset(const S& ss) { s = ss; } // reset state
private :
S s; // state
}class F 의 객체는 member s 라는 데이터를 hold 한다.
필요하다면, 함수 객체는 많은 데이터 멤버를 가질수있다.
"데이터를 가지고있다" 를 다른말로 "state 를 가지고있다" 라고도 한다.
우리가 F 를 만들때, 우리는 state 를 초기화할수있다.
우리가 원할때 언제든지 state 를 read 할수있다.
F 는 state() 함수를 통해 state 를 read 할수있고,
reset() 이라는 함수를 통해 write 할수있다.
하지만 우리가 함수 객체를 design 할때, state 를 접근하는 방법은 우리가 원하는 적절한 방법으로
제공하면 된다.
위의 코드에서 F 는 single argument 를 받지만, 우리가 원하는 많은 parameter 들로 설정할수도있다.
함수 객체의 사용은 STL 에서 매개변수화(parameterization) 를 구현하는데에 가장 중요한 방법이다.
함수 객체는 search (21.3), sort (21.4.2), 산술 연산과 숫자 알고리즘 (21.5) 등 많은곳에 사용된다.
함수 객체의 사용은 flexibility 와 generality 의 가장 주요한 source 이다.
함수 객체는 또한 매우 efficient 하다. 특히, template 함수에 함수 객체를 넘기는것은 성능을 향상시킨다.
함수 객체를 넘기는것이 함수를 넘기는것보다 엄청나게 훨씬 빠른 성능을 보장한다. (딴, 객체가 작을때만)
함수 객체의 사용이 좋은 성능을 갖는 이유는 compiler 가 최적의 code 를 생성하도록 충분한 type 정보를
보존하고있기때문이다.
21.4.2 Predicates on class members
앞서 보아왔듯이, standard 알고리즘들은 int 나 double 과 같은 기본 type 의 element sequence 와
잘 작동한다.
하지만, 대부분의 프로그램들에서는 사용자가 정의한 class 를 type 으로 갖는경우가 훨씬 허다하다.
아래와 같은 코드를 보자.
struct Record {
string name; // standard string for ease for use
char addr[24]; // old style to match database layout
};
vector<Record> vr;위의 코드에서, 우리는 어떨때는 name 으로 sort 하고싶을태고,
어떨때는 addr 로 sort 하고싶을것이다.
아래서 마저 설명...
21.4.3 Lambda expressions (람다 표현식)
내 프로그램에서 어느 부분에 단 한번 사용될 기능을 굳이 함수로 만드는것은 무의미한 일이다.
이럴때 사용하는것이 Lambda expressions (람다 표현식) 이다.
람다 표현식은 함수 객체를 정의하자마자 곧바로 사용하기위해 사용한다.
예를 보자.
/* sort 는 3번째 인자로 함수 객체를 받는다 */
sort(vr.begin(), vr.end(),
/* 여기에 바로 함수를 정의하고 곧바로 사용 */
[](const Record& a, const Record& b) {
return a.name < b.name;
}
);
sort(vr.begin(), vr.end()),
/* 여기에 바로 함수를 정의하고 곧바로 사용 */
[](const Record& a, const Record& b) {
return strncmp(a.addr, b.addr, 24) < 0;
}
);또다른 예.
auto p = find_if(v.begin(), v.end(), Large_than(31));
/* 위의 코드 대신에 */
/* 함수 객체가 들어갈 정리에 함수를 정의하고 바로 사용할수있다. */
auto p2 = find_if(v.begin(), v.end(), [](double a) { return a > 31; });21.5 Numerical algorithms
standard library가 제공하는 알고리즘 대부분은 data 관리(copy, sort, search 등등) 와 관련된것들이다.
하지만, 숫자를 compute 하는 4개의 알고리즘 역시 제공한다.
아래와 같이 정의후 사용할수있다.
#include <numeric>
21.5.1 Accumulate
가장 단순하고 유용한 numerical 알고리즘은 accumulate() (축적하다) 이다.
내부는 대략 아래와 같이 생겼다.
template<typename In, typename T>
T accumulate(In first, In last, T init) {
while (first != last) {
init = init + *first;
++first;
}
return init;
}init 이라는 첫 초기값부터, [first:last) 까지 모든 값을 더하여 sum 을 return 한다.
위의 코드에서 init 이 하는 역할을 accumulator (누산기, 축적기) 라고한다.
아래와 같이 사용할수있다.
int a[] = {1, 2, 3, 4, 5};
std::cout << accumulate(a, a + (sizeof(a) / sizeof(int)), 0); // 15
void g(int* p, int n) {
int s1 = accumulate(p, p + n, 0); // sum into an int
long s2 = accumulate(p, p + n, long {0}); // sum the ints into a long
double s2 = accumulate(p, p + n, 0.0); // sum the ints into a double
}늘 잊지말아야할것은 언제나 accumulate 의 3번째 인자인 accumulator 를 초기화해야한다는것이다.
double s1 = 0; // 초기화
s1 = accumulate(v.begin(), v.end(), s1);21.5.2 Generalizing accumulate()
accumulate() 는 기본적으로 "더하기" 이지만, 4번째 argument 로 우리가 원하는 연산을 직접 넘길수있다.
2개의 accumulator 를 인자로 받을수있는 어떠한 연산이든 올수있다.
이런 연산을 이항 연산자 (binary operator) 라고 한다.
내부 설계는 아래와 같다.
template<typename In, typename T, typename BinOp>
T accumulate(In first, In last, T init, BinOp op) {
while(first! = last) {
init = op(init, *first);
++first;
}
return init;
}아래와 같이 사용할수있다.
vector<double> a = {1.1, 2.2, 3.3, 4.4};
std::cout << accumulate(a.begin(), a.end(), 1.0, multiplies<double>()); // 1.0 * 1.1 * 2.2 * 3.3 * 4.4 (1.0 이 초기값)위에서 사용된 multiples<Type> 은 standard library 에서 제공하는 binrary operator 이다.
multiples 가 포함된 stadard library 는 <functional> 이다.
대략적으로 아래와 같은것들을 사용할수있다.
#include <functional>
multiples
plus
minus
divides
modulus
이번엔 우리가 직접 만든 함수를 넘기는 또다른 예제.
struct Record {
double unit_price;
int units;
}
double price(double v, const Record& r) {
return v + (r.unit_price * r.units);
}
void f(const vector<Record>& vr) {
double total = accumulate(vr.begin(), vr.end(), 0.0, price);
}
아래와 경우에 함수를 쓰는 대신 함수 객체를 사용하도록 하라.
-
call 간에 value 를 저장할 필요가 있을때.
-
매우 짧은 함수일때.
21.5.3 Inner product (내적)
2개의 벡터에서 동일한 subscript 의 각 element 를 서로 곱하여,
모두 더하는것을 두 벡터의 inner product (내적) 이라고한다.
내적은 많은 영역에서 매우 유용한 연산이다. (물리학, 선형 대수학 등등..)
STL 버전은 아래와 같다.
template<typename In, typename In2, typename T>
T inner_product(In first, In last, In2 first2, T init) {
while(first != last) {
init = init + (*first) * (*first2); // multiply pars of elements
++first;
++first2;
}
return init;
}아래와 같이 사용할수있다.
vector<double> dow_price = {81.86, 34.69, 54.45};
list<double>dow_weight = {5.8549, 2.4808, 3.8940};
double dji_index = inner_product (
dow_price.begin(), dow_price.end(), dow_weight.begin(), 0.0
);
std::inner_product 는 오직 3개의 인자만을 받는다.
주의해야할점은,
2번째 sequence (위에는 dow_weight) 의 길이가 최소한 첫번째 sequence (위에는 dow_price) 만큼
최소한 가지고있어야한다. 더 적을시 run-time error 가 발생한다.
첫번째 sequence 보다 2번째 sequence 가 더 많은것은 괜찮다.
더 많은 애들은 그저 연산에 사용되지않는다.
이 2개의 sequence 는 서로 동일한 type 일 필요가 없으며, (위에는 vector 와 list)
element 의 type 또한 동일하지않아도 된다.
이를 알려주기위해, 위 코드에서 vector 와 list 를 사용한것이다.
21.5.4 Generalizing inner_product()
template<typename In, typename In2, typename T, typename Binop, typename BinOp2>
T inner_product(In first, In last, In2 first2, T init, BinOp op, BinOp2 op2) {
while (first != last) {
init = op(init, op2(*first, *first2));
++first;
++first2;
}
return init;
}21.6 Associative containers
vector 이외에, standard library 에서 가장 유용한 container 는 map 이다.
map 는 key 와 value 로 이루어진 순서가 있는 sequence 이다.
우리는 value 를 key 로 찾을수있다.
unordered_map 은 key 를 string 으로 사용하기위해 최적화된 map 이다.
map 와 unordered_map 같이 유사한 자료구조를 묶어서,
associative arrays, hash tables, red-black trees 라고 한다.
모든 자료 구조를 통칭하여 associative containers 라고 한다.
standard library 는 아래의 8가지 associative containers 를 제공한다.

이 container 들은 <map>, <set>, <unordered_map>, <unordered_set> 으로 사용할수있다.
21.6.1 map
text 안에 단어의 발생갯수를 list 로 만든다고 가정해보자.
이를 위한 확실한 방법은, 우리가 새 단어를 보았을때,
이미 봤던 단어라면 count 를 1 추가하고, 본 단어가 아니라면 우리의 list 에 추가후 값을 1로 주는것이다.
list 와 vector 를 사용하여, 우리가 읽는 단어를 검색할수있다.
하지만 이 방법은 느릴것이다.
이럴때 map 을 사용해야한다.
void f() {
map<string, int> words; // keep (word, frequency) paris
for (string s; cin >> s;) {
++words[s]; // note : words is subscripted by a string
}
for (const auto& p : words) {
std::cout << p.first << ": " << p.scond << std::endl;
}
}위의 코드에서 주목해야할 부분은 ++words[s] 이다.
map<string, int> 의 의미는 string 을 int 로 map 한다는 뜻이다.
다시 말해, 주어진 string 으로 words 는 해당하는 int 를 접근할수있게 해주는것이다.
따라서, 우리는 words 를 string 으로 subscript 할수있다.
따라서 words[s] 는 s 에 해당하는 int 의 reference 이다.
++words[s] 는 우리가 input 으로 받는 word 를 받아 그 값을 1 증가시킨다.
만약 이 단어를 처음 보았다면, 값은 1 이 된다.
map<string, int> 는 다른 STL container 처럼 iterate 할수있으며,
각 element 는 pair<string, int> 이다.
각 pair 의 첫번째 member 를 first 라고 부르고, 두 번째 member 를 second 라고 한다.
따라서 아래와 같은 코드가 가능하다.
for (const auto& p : words) {
std::cout << p.first << ": " << p.scond << std::endl;
}아래와 같은 text 를 받았다고 치자.

output 으로 아래와 같이 출력된다.

21.6.2 map overview
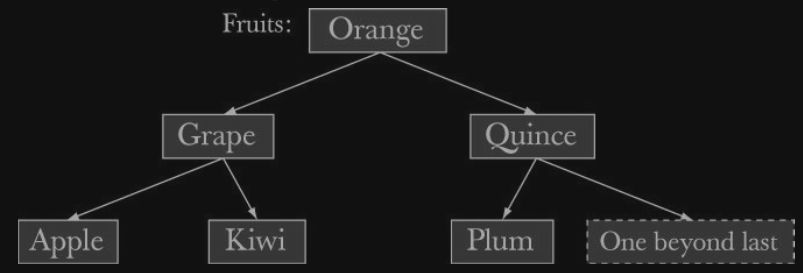
STL map 의 내부는 binrary search tree (red-black tree) (이진탐색트리) 로 구현되어있다.
하나의 tree 는 다수의 node 들로 이루어진다.
이 tree 안에 각 node 는 key, value, 그리고 후손 node 들을 가리키는 2개의 pointer 로 이루어져있다.
그림으로 보면 아래와 같다.

예를 들어, map<Fruit, int> 에 (Kiwi, 100), (Quince, 0), (Plum, 8), (Apple, 7), (Grape, 2345), (Orange, 99)
를 insert 했다고 가정해보자.
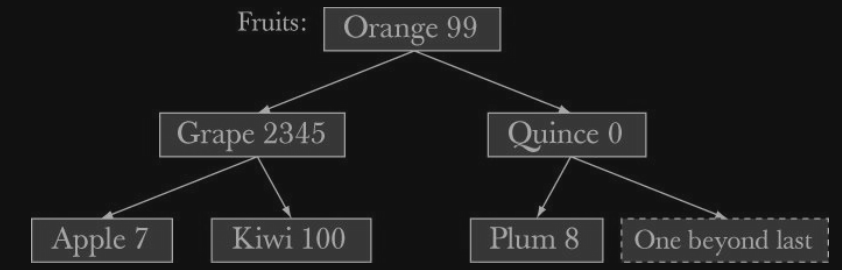
map 에서는 각 key 값의 크고작음음을 서로 비교할수있다.
주요 원칙은 아래와 같다.

-
왼쪽 sub node 의 key 는 자신의 key 보다 작다.
-
오른쪽 sub node 의 key 는 자신의 key 보다 크다.
위의 원칙이 tree 의 root 부터 아래로 검색해나갈수있도록 해준다.
컴퓨터 과학에서 tree 는 자신의 root 로부터 아래방향 (downward) 하게 되어있다.
따라서, 우리는 tree 의 아래방향으로 우리가 원하는 것을 찾을때까지 내려간다.
위의 그림은 한 node 가 2개의 sub tree 를, 그 sub tree 각각이 다시 2개의 sub tree 를 가지고있는데,
이와 같은 tree 를 balanced 라고 한다.
balanced 가 되는것은 우리가 원하는 node 에 도달하기까지 방문해야할 node 의 갯수를 최소화해준다.
Node 는 map 이 node 의 tree 가 balanced 함을 유지하기위해 더 많은 data 를 가지고있을수도있다.
각 node 가 오른쪽의 후손 갯수만큼 왼쪽도 가지고있어야 tree 는 balanced 된다.
우리는 대부분 node 를 찾기위해 log2(N) 을 사용해야한다.
아래는 unbalanced tree 이다.
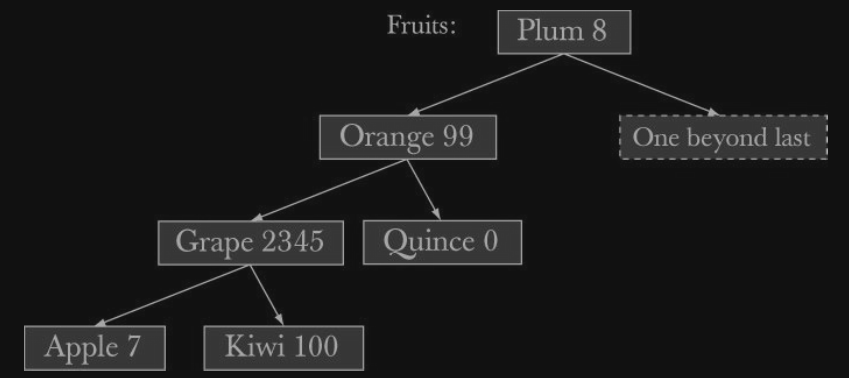
위의 tree 는 여전히 각 node 의 key 가 왼쪽 sub node 보다는 크고, 오른쪽 sub node 보다는
작아야한다는 기준을 충족한다.

하지만 위의 tree 는 unbalance 하기때문에,
우리가 Apple 과 Kiwi 에 도달하기까지 3개를 거쳐야한다. (balanced tree 는 2개를 거치는것에 반해)
많은 node 를 가진 tree 가 "unbalance 이냐 balance 이냐" 는
성능에서 매우 큰 차이를 나타낸다.
따라서 map 을 구현하기위해 사용된 tree 는 balance 이다.
우리가 map 을 사용함에 있어, tree 를 이해하는것이 필수는 아니다.
하지만 우리가 프로페셔널 프로그래머가 되기위해서 자신이 사용하는 도구의 fundamental 을
이해하는것이 합리적이다.
map 의 대략적인 내부 interface 는 아래와 같다.
template<typename T1, typename 2>
struct pair {
using first_type = T1;
using second_type = T2;
T1 first;
T2 second;
};
template<typename T1, typename T2>
pair<T1, T2> make_pair(T1 x, T2 y) {
return {x, y};
}
template<typename Key, typename Value, typename Comp = less<Key>>
// requires Binrary_operation<Cmp, Value>()
class map {
using value_type = pair<Key, Value>; // a map deals in (Key, Value) pairs
using iterator = sometype1; // similar to a pointer to a tree node.
using const_interator = sometype2;
iterator begin(); // points to first element
iterator end(); // points one beyond the last element
Value& operator[](const Key& k); // subscript with k
iterator find(const Key& k); // is there an entry for k?
void erase(iterator p); // remove element pointed to by p
pair<iterator, bool> insert(const value_type&); // insert a (key, value) pair
};기억해야할것은, map 을 iterate 할때,
element 는 key 에 의해 정의된 순서에 따라 접근된다.
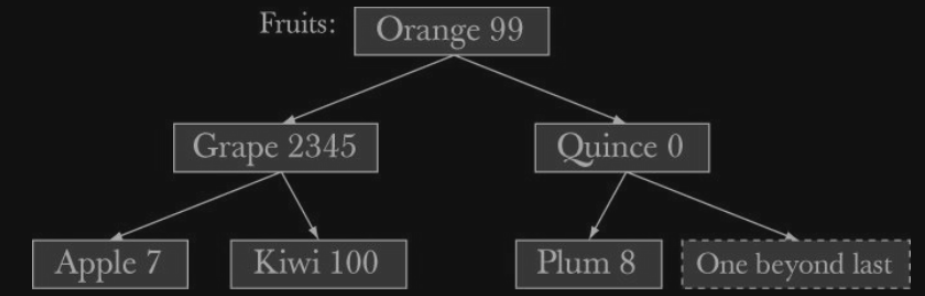
위와 같은 구조라고 치면, 아래와 같은 순서이다.

우리가 insert 하는 순서에 따라 나열되는것이 아니라는것이다.
하지만 map 의 3번째 인자에 어떤 순서로 나열될지를 정의할수있다.
예를 들어,
map<string, double, No_case> m;위와 같이 작성하였다면, 대소문자를 구분하지않고 배열된다.
21.6.3 Another map example
map 을 사용하는 가장 공통적인 이유는 우리는 key 로 value 를 얻고싶기때문이다.
매우 큰 sequence 에서 find() 를 사용하는것은 map 보다 훨씬 느릴것이다.
21.6.4 unordered map
vector 에서 element 를 찾기위해 사용하는 find() 함수는,
vector 의 시작부터 값을 찾을때까지 끝까지 진행한다.
이때드는 비용은 vector 의 길이와 비례한다.
반면, map 에서 element 를 찾기위해서 사용하는 subscript [ ] 연산자는
tree 의 root 부터 원하는 값을 찾을때까지 잎사귀로 진행한다.
이때드는 비용은 map 의 depth (깊이) 에 비레한다.
balance 인 tree 가 N 개의 element 를 가지고있다고 가정하면,
최대 depth 는 log2(N) 이며, vector 에 비해 비용의 증가율이 훨씬 적다.
하지만 실제 비용은 우리가 원하는것을 얼마나 빨리 찾는지에 따라,
또는 비교와 iteration 이 얼마나 비싼지에 따라 다르다.
보통 pointer 를 추적하는것 (map 의 look up 방법) 이
pointer 를 증가시키는것 (vector 의 find()) 보다 훨씬 비싸다.
string 이나 int 같은 type 의 경우 map 에서 훨씬 빠른 tree 검색을 할수있다.
vector 에서는 index 를 사용하는데 이 index 를 hash value 라고 부르며,
이 hash value 를 사용하는 container 를 hash table 이라고 한다.
key 로 가능한것들의 숫자가 hash table 의 slot 의 숫자보다 훨씬 크다.
예를 들어, 우리는 자주 십억개의 가능한 string 을 1000개의 element 를 가진 vector 의 index 로
map 하기위하여 hash 함수를 사용한다.
hash table 의 가장 큰 장점은 look up 하는 비용이 매우 일정하며,
table 의 element 의 갯수와 독립적이다.
각 container 가 look up 하는 방법을 그림으로 보면 아래와 같다.
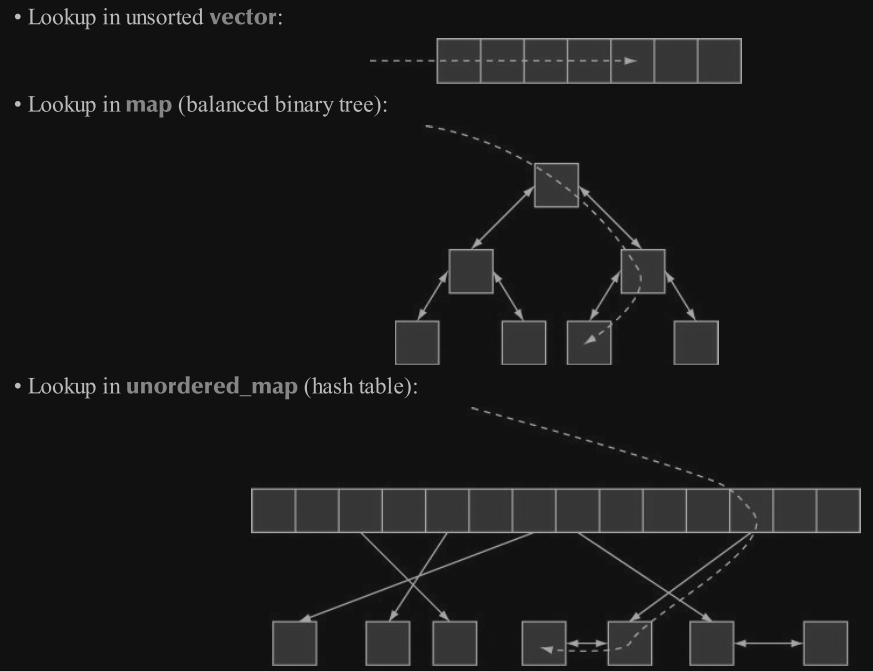
-
unordered_map : hash table 을 사용
-
map : balanced binary tree 를 사용
-
vector : array 를 사용
이 셋중에 무엇을 언제 사용해야됩니까?
-
vector : 사용하지않을 이유가 있지않는한 사용하라.
-
map : value 에 기반하여 look up 하고싶다면 사용하라.
-
unordered_map : 매우 큰 map 에서 엄청나게 자주 look up 하고, 각 element 에 순차적인 순회가 필요없다면 사용하라.
map 과 unordered_map 의 사용법은 동일하지만,
unordered_map 은 iterate 할때 element 가 순서대로 나오지않는다.
21.6.5 set
set 는 value 에 관심이 없는 map 이라고 생각하면 된다.
set 의 node 는 아래와 같다.

set 은 value 가 없기때문에 subscript 를 지원하지않는다.
우리는 insert() 나 erase() 같은 list operation 을 사용해야한다.
불행히도 map 과 set 은 push_back() 을 지원하지않는다.
이유는 프로그래머가 아닌 set 이 새로운 값이 어디에 insert 될지 결정하기때문이다.
따라서 insert() 를 사용하라.
set 이 map 보다 좋은 점은 iterator 를 직접적으로 사용할수있다는것이다.
map 처럼 pair(key, value) 로 되어있지않기때문에.
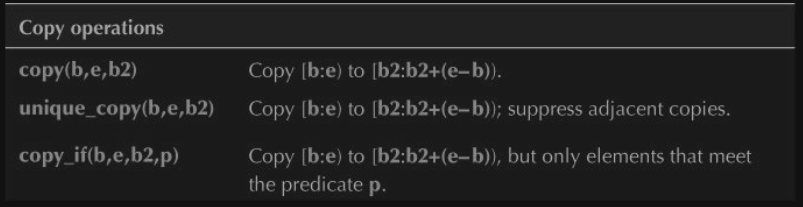
21.7 Copying
STL 은 3가지의 copy 를 제공한다.
21.7.1 Copy
copy 의 내부는 아래와 같다.
template<typename In, typename Out>
Out copy(In first, In last, Out res) {
while (first != last) {
*res = *first; // copy element
++rest;
++first;
}
return res;
}copy() 는 첫번째 element 를 가리키는 iterator 에 의해 한 sequence 에서 다른 sequence 로 복사한다.
void f(vector<double>& vd, list<int>& li) {
copy(li.begin(), li.end(), vd.begin());
}위의 코드처럼, input sequence 와 output sequence 의 type 이 다를수있다.
이런점이 STL 알고리즘의 유용함이다.
STL 알고리즘은 일반성을 극대화하고 최적의 성능을 내도록 설계되었다.
이 알고리즘은 default 로 range-check 이나 사용자를 보호하기위한 비싼 test 를 하지않는다.
이런 test 나 check 은 사용자가 스스로 추가해야한다.
21.7.2 Stream iterators
생략.
21.7.3 Using a set to keep order
생략.
21.7.4 copy_if()
copy() 는 조건없이 copy 하는데에 반해,
unique_copy() 는 동일한 element 에 같은 값을 복사하는것을 막는다.
오직 predicate 가 true 일때만 element 를 copy 한다.
template<typename In, typename Out, typename Pred>
Out copy_if(In first, In last, Out res, Pred p) {
while (first != last) {
if (p(*first)) {
*res++ = *first;
++first;
}
}
return res;
}
21.8 Sorting and searching
21.9 Container algorithms
생략.
Review
-
What are examples of useful STL algorithms?
-
What does find() do? Give at least five examples.
-
What does count_if() do?
-
What does sort(b, e) use as it's sorting criterion?
-
How does an STL algorithm take a container as an input argument?
-
How does an STL algorithm take a container as an output argument?
-
How does an STL algorithm usually indicate "not found" or "failure"?
-
What is a function object?
-
In which ways does a function object differ from a function?
-
What is a predicate?
-
What does accumulate() do?
-
What does inner_product() do?
-
What is an associative container? Give at least three examples.
-
Is list an associative container? Why not?
-
What is the basic ordering property of binrary tree?
-
What (roughly) does it mean for a tree to be balanced?
-
How much space per element does a map take up?
-
How much space per element does a vector take up?
-
Why would anyone use an unordered_map when an (ordered) map is available?
-
How does a set differ from a map?
-
How des a multimal differ from a map?
-
Why use a copy() algorithm when we could "just write a simple loop"?
-
What is a binary search?
Terms
-
accumulate()
-
algorithm
-
application : ()
-
associative container
-
balanced tree
-
binrary_search()
-
copy()
-
copy_if()
-
equal_range()
-
find()
-
find_if()
-
function obejct
-
generic
-
hash function
-
inner_product()
-
lambda
-
lower_bound()
-
map
-
predicate
-
searching
-
sequence
-
set
-
sort()
-
sorting
-
stream iterator
-
unique_copy()
-
unordered_map
-
upper_bound()




